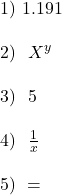Kiedy średnia nie uśrednia, czyli jak policzyć swoje zyski i dlaczego wiele osób robi to źle

Rozmawiałem kiedyś z przedstawicielem domu maklerskiego, który pokazywał mi wyniki swojego portfolio o oszałamiającej stopie zwrotu z ostatnich pięciu lat na poziomie około 50% rocznie. Robi wrażenie, prawda? Na mnie też zrobiło, dlatego zacząłem drążyć temat i okazało się, że…

Nieco to teraz uproszczę, bo metodologia liczenia zysków zastosowana przez owego pana była nieco bardziej finezyjna, ale ostatecznie sprowadzała się do postaci, którą zaraz tu wyciągnę na światło dzienne i rozłożę na czynniki pierwsze.

Wyobraź sobie, że kupujesz akcje o wartości 10 000 zł, które po pierwszym roku inwestycji rosną do 20 000 zł. Jednak po drugim roku ich wartość spada znowu do 10 000 zł. Jakie procentowo zyski osiągnąłeś średnio w skali jednego roku?

Na pohybel średniej (arytmetycznej)

Najprościej można odpowiedzieć na to pytanie sumując procentowe zyski z obu lat i dzieląc je przez liczbę tych lat. W ten sposób wyliczymy prostą średnią arytmetyczną z rocznych zysków.

Tak więc po pierwszym roku kwota 10 000 zł zamieniła się w kwotę 20 000 zł, a więc pierwszego roku zysk wyniósł 100%. Drugiego roku 20 000 zł zamieniło się w 10 000 zł, a więc strata wyniosła 50%. Sumując te dwa wyniki i dzieląc je przez liczbę lat, których dotyczą, otrzymamy średnią roczną stopę zwrotu na poziomie 25%.

Od strony matematyki wszystko jest w porządku. Tylko że od strony intuicji coś tu jednak się nie zgadza. Skoro w naszym przykładzie średnio rocznie zarabiamy 25%, to dlaczego u diabła po dwóch latach ciągle jesteśmy „na zero”?

Dzieje się tak dlatego, że średnia arytmetyczna zakłamuje wyniki w przypadku, gdy mamy do czynienia z giełdowymi inwestycjami. Zwykła średnia nie działa właściwie w żadnym przypadku, w którym do gry wchodzi zjawisko zwane procentem składanym.

Nie trzeba być matematykiem, żeby olśnienie zapukało nam w tym momencie do głowy i zapytało: Co z tego, że pierwszego roku zarobiłeś aż 100%, a drugiego roku straciłeś tylko 50%, skoro 100% zysku policzone zostało od kwoty dwa razy mniejszej niż 50% straty?

W tym akurat przypadku gołym okiem widać, że coś tu nie gra, ponieważ mamy do czynienia z okrągłymi liczbami i ze znacznymi różnicami procentowymi. W rzeczywistym świecie, kiedy zawieramy setki transakcji i kiedy mamy do czynienia z różnicami procentów zapisywanych z dokładnością do drugiego miejsca po przecinku, wcale nie tak łatwo jest zorientować się, że popełniamy błąd w analizie wyników (albo że ktoś celowo próbuje nimi manipulować).

Nowa miara w mieście (geometryczna)

Aby poprawnie wyliczyć łączne zyski z jakichkolwiek inwestycji, należy zastosować średnią geometryczną, która weźmie pod uwagę działanie procenta składanego.

Teoretycznie wzór na średnią geometryczną wygląda tak:

gdzie X oznacza każdy kolejny pojedynczy procentowy zysk w skali konkretnego roku, a N liczbę lat, z których liczymy średnią.

Jednak żeby wyliczenie tego wzoru się udało, każda składowa równania musi być dodatnia, dlatego najpierw należy zamienić procenty na wartości liczbowe (podzielić je przez 100), a następnie dodać do nich jedynkę, którą potem odejmiemy już po wykonaniu mnożenia.

100% dzielimy przez 100 i zapisujemy jako 1, natomiast -50% podzielone przez 100 zapisujemy jako -0.50. Potem do każdego elementu dodajemy 1, a więc mamy odpowiednio: 2 oraz 0.50.

Teraz możemy podstawić te liczby do wzoru:

Pierwiastek kwadratowy z 1 to też 1, ale teraz trzeba jeszcze odjąć drugą jedynkę, którą na początku dodaliśmy, żeby nie dopuścić do mnożenia przez ujemne liczby.

Ostatecznie więc nasz wzór wygląda tak:

Otóż to. Średnia geometryczna pokazuje, że w naszym przykładzie osiągnęliśmy średni roczny zysk w wysokości… 0%. Jest to o wiele bardziej adekwatne wskazanie, niż wynik otrzymany za pomocą średniej arytmetycznej. Po dwóch latach dalej mamy bowiem w portfelu 10 000 zł, czyli dokładnie taką samą kwotę, z jaką zaczynaliśmy inwestycje.

Zweryfikujmy to na bardziej rozbudowanym przykładzie:

• Wynik portfela po pierwszym roku: 13%
• Wynik portfela po drugim roku: -5%
• Wynik portfela po trzecim roku: 9%
• Wynik portfela po czwartym roku: 17%
• Wynik portfela po piątym roku: -13%

Średnia arytmetyczna powie nam tutaj, że rocznie osiągamy zysk 4.2%:

To spróbujmy w takim razie wyliczyć bardziej poprawną średnią geometryczną, która uwzględni procent składany. Najpierw zamieniamy wszystkie procenty na wartości liczbowe, a następnie dodajemy do każdej z nich 1:

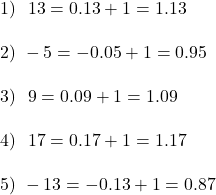
Teraz mnożymy przez siebie wszystkie powyższe wartości, a potem obliczamy pierwiastek piątego stopnia i na końcu odejmujemy od wyniku jedynkę, którą dodaliśmy na początku. Żeby otrzymaną na końcu liczbę zamienić na procenty, wystarczy pomnożyć ją przez 100.

A więc średnia geometryczna mówi, że nasz portfel w trakcie pięciu lat uzyskał realny roczny zwrot w wysokości 3.55%.

Jak obliczyć taki pierwiastek na kalkulatorze?

Jeśli kalkulator posiada przycisk , to wystarczy wpisać wartość 1.191, kliknąć przycisk , następnie wcisnąć „5”, a potem „=”.

Jeśli kalkulator nie posiada przycisku , to można zastosować inny trik. Pierwiastek piątego stopnia będzie bowiem tym samym, co podniesienie danej liczby do potęgi odwrotności tego stopnia, czyli do jego ułamka.

da taki sam wynik co .

Żeby więc obliczyć na kalkulatorze pierwiastek piątego stopnia w sposób alternatywny można wcisnąć następującą sekwencję klawiszy w pięciu krokach:

Wynik powinien być taki sam, co przy wyciąganiu pierwiastka piątego stopnia, czyli w zaokrągleniu 1.0355, co z kolei po odjęciu jedynki i pomnożeniu przez 100 daje 3.55%.

W internecie znaleźć można sporo darmowych kalkulatorów do obliczania średniej geometrycznej i procenta składanego, ale znając oryginalny wzór, można go teraz śmiało podstawić do swojego arkusza kalkulacyjnego, w którym śledzimy postępy na giełdzie.

Problem dodatkowej gotówki

Obliczenie średniej geometrycznej da poprawne wyniki pod warunkiem, że w trakcie trwania inwestycji nie dopłacaliśmy do portfela żadnych dodatkowych środków. W praktyce jednak często sytuacja wygląda inaczej.

Wyobraźmy sobie, że zaczynamy rok z akcjami pojedynczej firmy o wartości 10 000 zł. W drugim kwartale dopłacamy do portfela 1500 zł i dokupujemy akcje tej samej firmy. W trzecim kwartale dopłacamy 2000 zł i dokupujemy akcje nowej firmy, a w czwartym kwartale wpłacamy aż 4000 zł, ale nie kupujemy jeszcze żadnych akcji.

Jeśli na koniec roku chcielibyśmy policzyć jakie zyski udało nam się wypracować, to w takim wypadku nie wystarczy po prostu odjąć początkowej wartości całego portfela według stanu na 1 stycznia od końcowej wartości według stanu na 31 grudnia i wyciągnąć z tego procenta.

Takie wyliczenie nic nam nie powie o naszej skuteczności na giełdzie w danym roku, bo dodatkowe wpłacane środki nie miały jeszcze pełnego roku na to, aby wypracować jakikolwiek zysk, a więc włączanie ich w ten sposób do rocznych statystyk jest niepoprawne i przekłamuje rzeczywistość.

Oto, co powinniśmy zrobić

Aby w pełni oddać nasze rzeczywiste osiągnięcia, przed każdą nową wpłatą do portfela musimy policzyć jego wynik od początku danego okresu do tego konkretnego momentu.

Dzień każdej nowej wpłaty będzie resetem licznika i zabawa zacznie się na nowo. W ten sposób powinniśmy robić za każdym razem w trakcie całego roku, kiedy tylko do portfela dopłacamy lub wypłacamy z niego pieniądze.

W praktyce może to wyglądać tak:

• 1 stycznia – wpłata 10 000 zł i kupno akcji
• 31 marca – podsumowanie wyników kwartału i reset licznika
• 1 kwietnia – wpłata 1500 zł i kupno akcji
• 31 czerwca – podsumowanie wyników kwartału i reset licznika
• 1 lipca – wpłata 2000 zł i kupno akcji
• 31 września – podsumowanie wyników kwartału i reset licznika
• 1 października – wpłata 4000 zł
• 31 grudnia – podsumowanie wyników czwartego kwartału i całego roku, a potem reset licznika

Podsumowanie kwartałów powinno przebiegać tak:

• Początek Q1 – Wartość początkowa na 1 stycznia: 10 000 zł
• Koniec Q1 – Wartość portfela na 31 marca: 12 300 zł. Zysk kwartalny: 23%
• Początek Q2 – Wartość początkowa na 1 kwietnia: 13 800 zł (12 300 + 1500)
• Koniec Q2 – Wartość portfela na 31 czerwca: 11 700 zł. Zysk kwartalny: -15.22%
• Początek Q3 – Wartość początkowa na 1 lipca: 13 700 zł (11 700 + 2000)
• Koniec Q3 – Wartość portfela na 31 września: 14 100 zł. Zysk kwartalny: 2.9%
• Początek Q4 – Wartość początkowa na 1 października: 18 100 zł (14 100 + 4000)
• Koniec Q4 – Wartość portfela na 31 grudnia: 20 000 zł. Zysk kwartalny: 10.5%

Na tym przykładzie łatwo dostrzec jak bardzo wypaczone wyniki mogą powstać biorąc pod uwagę jedynie ujęcie kwotowe w skali całego roku, a nie biorąc pod uwagę częściowych dopłat gotówkowych.

Gdybyśmy spojrzeli bowiem wyłącznie na to, że na początku roku wartość portfela wynosiła 10 000 zł, a na koniec roku 20 000 zł, można by wysnuć wniosek, że nasz roczny zysk to 100%. To jednak błędne obliczenie.

Aby sprawdzić jaki rzeczywiście wynik osiągnęliśmy z uwzględnieniem wpłat gotówkowych, należy wyliczyć średnią geometryczną złożoną z poszczególnych okresów.

Tym razem zrobimy to jednak nieco inaczej niż w przypadku średniej z wielu różnych lat. Tutaj średnia będzie liczona wyłącznie w skali jednego roku, a więc nie będzie potrzeby używania pierwiastka.

Cała reszta metodologii pozostaje jednak taka sama, a więc: 

1. Zamieniamy procenty na wartości liczbowe (można to zrobić dzieląc je przez 100, albo po wpisaniu wartości na kalkulatorze, klikając przycisk: %)
2. Do każdego wyniku z osobna dodajemy 1
3. Mnożymy przez siebie wszystkie pojedyncze wyniki
4. Od sumy odejmujemy jedynkę
5. Mnożymy wynik razy 100

Najpierw więc zamiana procentów na liczby i dodanie jedynki:

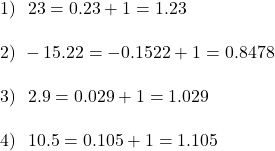
Mała dygresja: żeby na kalkulatorze wpisać liczbę ujemną, np. -15.22, wystarczy wpisać 15.22 i wcisnąć przycisk: +/-

Potem pomnożenie procentów przez siebie i odjęcie jedynki oraz zamiana liczbowego wyniku na zapis procentowy:

A więc poprawny wynik uwzględniający wszystkie wpłaty gotówkowe pokazuje, że w trakcie tego roku nasz portfel wypracował 18.57% zysku.

To delikatna różnica w stosunku do zarobku 100%, który można by stwierdzić na pierwszy rzut okna po podsumowaniu początkowego i końcowego salda na rachunku maklerskim.

Teraz mając policzony taki jednostkowy „uczciwy” roczny zysk, będzie można go później zestawić z tak samo porachowanym zyskiem z kolejnych lat, aby przy pomocy średniej geometrycznej (tej z pierwiastkiem) wyliczyć, ile tak właściwie nasz portfel przeciętnie zarabia w skali roku, na przestrzeni wielu lat.

To najbardziej poprawny sposób wskazujący prawdziwe osiągnięcia portfolio i nie pozwalający na żadne manipulacje wynikami, które chętnie stosują wszelkiej maści naciągacze.